Есть массив с данными в виде:
data =
{{{2011, 3, 29, 22, 1, 2}, 15},
{{2011, 3, 29, 22, 11, 38}, 900},
{{2011, 3, 29, 22, 14, 21}, 654},
{{2011, 3, 29, 22, 18, 3}, 1},
{{2011, 3, 29, 22, 20, 31}, 934},
{{2011, 3, 29, 22, 30, 36}, 11},
{{2011, 3, 29, 22, 38, 16}, 72},
... ... ... ...
{{2011, 3, 29, 23, 39, 36}, 258},
{{2011, 3, 29, 23, 51, 51}, 31},
{{2011, 3, 29, 23, 57, 57}, 939},
{{2011, 3, 29, 23, 58, 33}, 513},
{{2011, 3, 29, 23, 59, 4}, 178}}
Т.е. первая колонна время начала события, вторая - продолжительность.
Как построить график из колонн где ширина колонны это диапазон например в 30 минут а высота колонны это общая продолжительность событий в диапазоне.
Изначально данные через DateListPlot[] выглядят так:
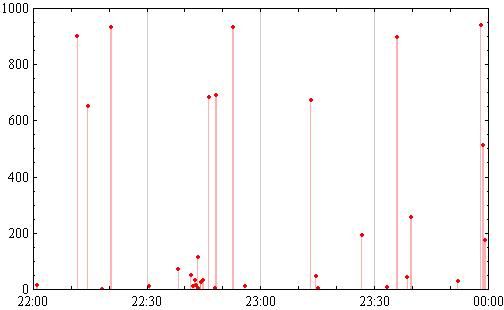
Нужно добавить BarChart[] или другую альтернативу (которая собстенно и ищется)
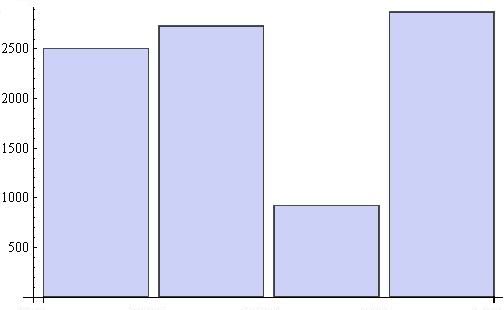
Для получения следующего результата:
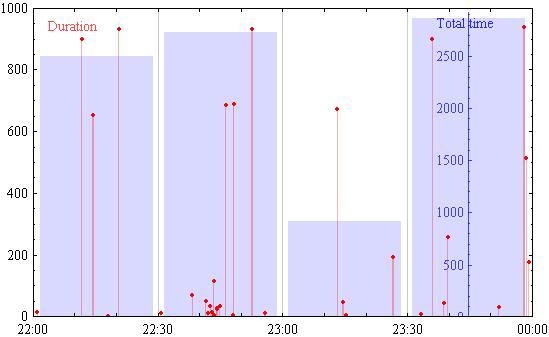
Основная проблема в том что как только событий становится больше пары тысяч - стандартные методы расчёта высоты колонны суммируя группу значений попадающих в необходимый диапазон // через Total[Table[Select[data,end[_n]>=#[[1]]>=start[_n]&],{n,1,..}][[All,2]]] // занимает слишком много времени на какие-то преобразования (частично думаю из-за преобразования с оператором AbsoluteTime[{2011, 3, 29, 23, 59, 4}] для подгонки возможности параметров сравнения попадания в диапазон)
Я реализовывал через следующие операции:
Начало и первый график:
"end time";
et0d={{2011,3,30,0,0,0}};
"start time";
st0d={DateList[et0d[[1]]-{0,0,0,2,0,0}]};
"to absolute time";
dataabs=Transpose[{Table[AbsoluteTime[data[[All,1]][[n]]],{n,1,Length[data]}],data[[All,2]]}];
"Plot with dots";
DateListPlot[dataabs,PlotRange->{{st0d[[1]],et0d[[1]]},{0,1000}},PlotStyle->{Red},Filling->Axis,FillingStyle->Directive[Red,Opacity[0.3]]]
Второй график:
"------------- start of time/duration conversion to bars (via total)------------";
bar=Table[Select[dataabs,AbsoluteTime[st0d[[1]]]+((n-1)*(AbsoluteTime[et0d[[1]]]-AbsoluteTime[st0d[[1]]])/4)<=#[[1]]<=AbsoluteTime[st0d[[1]]]+(n*(AbsoluteTime[et0d[[1]]]-AbsoluteTime[st0d[[1]]])/4)&],{n,1,4}];
barb=Table[Total[bar[[n]][[All,2]]],{n,1,4}];
BarChart[barb]
"---------------end of time/duration conversion to bars (via total)--------------";
Реализация третьего графика:
DateListPlot[dataabs,
__PlotRange->{{st0d[[1]],et0d[[1]]},{0,1000}},
__ImageSize->{400,250},
__PlotStyle->{Red},
__Filling->Axis,
__FillingStyle->Directive[Red,Opacity[0.3]],
__Prolog->Inset[
____BarChart[barb,
____ImageSize->{400,225},
____Axes->{False,True},
____AxesOrigin->{Length[barb],0},
____AxesStyle->Directive[Blue,Opacity[0.7]],
____ChartStyle->Directive[Opacity[0.15],Blue,EdgeForm[]]
___],Scaled[{0.5,0.48}]],
__Epilog->{Inset[Style["Duration",Red,Opacity[0.7]],Scaled[{0.08,0.94}]],
_________ Inset[Style["Total time",Blue,Opacity[0.8]],Scaled[{0.865,0.95}]]
__}]
Какие есть альтернативы (кроме вставки PerformanceGoal->"Speed" ) быстрого получения из данных с датой и продолжительностью в что-то похожее на такой BarChart.
Спсб.
Я пару раз открыл файл с расширением .m и вес дальнейший интерес/любопытство тут-же пропало..
